An Analysis of Cardano’s Formula to Solved Cubic Equation

Abstract

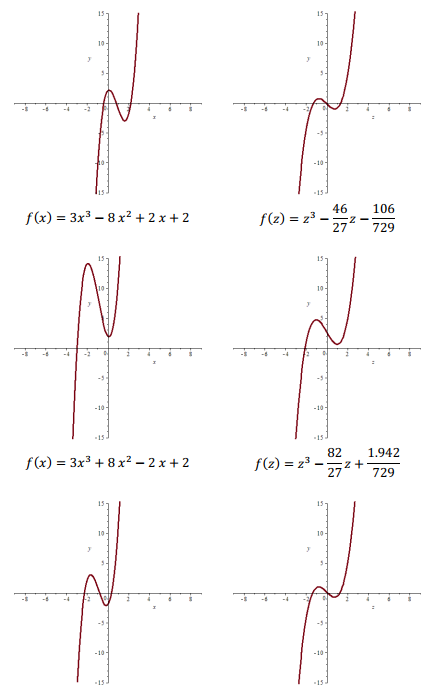
Cubic equation in complex is equation with the form az³ + bz² + cz + d = 0, . The equation has solution that is often referred to as the root of the equation. In the method commonly is used to find the root of the equation is usually obtained the real number, but for complex root it can’t be determined. In determined the complex root is used Cardano’s formula. This formula is reduced the form of the cubic equation to canonical equation form, namely z³ + pz + q = 0. This research a basic research. In this research data was collected from various sources in the form of related theories. Beginning with analyzing the graph and it characteristics, tracing the Cardano’s formula and analyzing it proof. Furthermore, is formed a formula with the characteristics of the roots owned by a cubic equation. The research results show that Cardano’s formula which has root for can be determined of the roots with values of and . The characteristics of the roots of cubic equation z³ + pz + q = 0 are depended by the values of p, q and , where . Thus, eight characteristics of the roots of cubic equation can be obtained based on the values of p, q and .