Exploring Students’ Mathematical Representation through the Lens of APOS Theory of APOS Theory: An Exploratory Study

Abstract

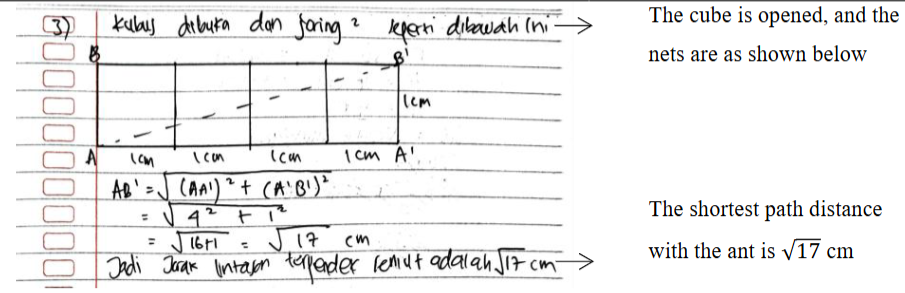
Mathematical representation ability is one of the key competencies that reflects the depth of students’ conceptual understanding in mathematics learning. However, various studies show that mathematics education students still face difficulties in using and connecting multiple forms of representation, leading to limited conceptual understanding. This study aims to analyse students’ mathematical representation abilities using the APOS (Action, Process, Object, Schema) theoretical framework to reveal the underlying mental mechanisms. A qualitative descriptive method with data triangulation (test and interview) was employed. Six mathematics education students were selected and categorized into low (score < mean – SD), medium (mean – SD ≤ score < mean + SD), and high (score ≥ mean + SD) ability groups based on their mathematical representation test results. Data from tests and interviews were analysed through qualitative coding to ensure reliability and credibility. The findings indicate that low-ability students tended to remain at the Action stage, medium-ability students reached the Process stage, and high-ability students began to reach the Object and Schema stages. This study confirms that the quality of mathematical representation is closely related to students’ cognitive stages according to the APOS theory and introduces a novel link between representation indicators and APOS stages, offering valuable insights for mathematics education research.